1
For this project, I worked with several colleagues in Boulder, Colorado, to apply what we understood of educational theory and approaches to computer support of collaboration to the plight of classroom teachers. Constructivist approaches to learning were well established as being favored by most educational researchers. The problem was to disseminate this to teachers in the actual classrooms. Even when teachers were trained in the theory, they had no practical instructional materials to implement the new approach on a daily basis. There were few textbooks or other resources available; even if materials were located, the teachers would still have to spend vast amounts of time they did not have to integrate them into the classroom practices and the institutional requirements.
The Internet was just starting to reach public schools, so we tried to devise computer-based supports for disseminating constructivist resources and for helping teachers to practically adapt and apply them. We prototyped a high-functionality design environment for communities of teachers to construct innovative lesson plans together, using a growing database of appropriately structured and annotated resources. This was an experiment in designing a software system for teachers to engage in collaborative knowledge building.
This study provides a nice example of a real-world problem confronting teachers. It tries to apply the power of AI and domain-oriented design environment technologies to support collaboration at a distance. The failure of the project to go forward beyond the design phase indicates the necessity of considering more carefully the institutional context of schooling and the intricacies of potential interaction among classroom teachers.
Introduction
Many teachers yearn to break through the confines of traditional textbook-centered teaching and present activities that encourage students to explore and construct their own knowledge. But this requires developing innovative materials and curriculum tailored to local students. Teachers have neither the time nor the information to do much of this from scratch.
The Internet provides a medium for globally sharing innovative educational resources. School districts and teacher organizations have already begun to post curriculum ideas on Internet servers. However, just storing unrelated educational materials on the Internet does not by itself solve the problem. It is too hard to find the resources to meet specific needs. Teachers need software for locating material-rich sites across the network, searching the individual curriculum sources, adapting retrieved materials to their classrooms, organizing these resources in coherent lesson plans and sharing their experiences across the Internet.
In response to these needs, I designed and prototyped a Teacher’s Curriculum Assistant (TCA) that provides software support for teachers to make effective use of educational resources posted to the Internet. TCA maintains information for finding educational resources distributed on the Internet. It provides query and browsing mechanisms for exploring what is available. Tools are included for tailoring retrieved resources, creating supplementary materials and designing innovative curriculum. TCA encourages teachers to annotate and upload successfully used curriculum to Internet servers in order to share their ideas with other educators. In this chapter I describe the need for such computer support and discuss what I have learned from designing TCA.
The Internet’s Potential for Collaboration Support
The Internet has the potential to transform educational curriculum development beyond the horizons of our foresight. In 1994, the process was just beginning, as educators across the country started to post their favorite curriculum ideas for others to share. Already, this first tentative step revealed the difficulties inherent in using such potentially enormous, loosely structured sources of information. As the Internet becomes a more popular medium for sharing curricula, teachers, wandering around the Internet looking for ideas to use in their classrooms, confront a set of problems that will not go away on its own¾on the contrary:
1. Teachers have to locate sites of curriculum ideas scattered across the network; there is currently no system for announcing the locations of these sites.
2. They have to search through the offerings at each site for useful items. While some sites provide search mechanisms for their databases, each has different interfaces, tools and indexing schemes that must be learned before the curricula can be accessed.
3. They have to adapt items they find to the needs of their particular classroom: to local standards, the current curriculum, their own teaching preferences and the needs or learning styles of their various students.
4. They have to organize the new ideas within coherent curricula that build toward long-term pedagogical goals.
5. They have to share their experiences using the curriculum or their own new ideas with others who use the resources.
In many fields, professionals have turned to productivity software—like spreadsheets for accountants—to help them manage tasks involving complex sources of information. I believe that teachers should be given similar computer-based tools to meet the problems listed above. If this software is designed to empower teachers¾perhaps in conjunction with their students¾in open-ended ways, opportunities will materialize that we cannot now imagine.
In this chapter, I consider how the sharing of curriculum ideas over the Internet can be made more effective in transforming education. I advance the understanding of specific issues in the creation of software designed to help classroom teachers develop curricula and increase productivity, and introduce the Teacher’s Curriculum Assistant (TCA) that I built for this purpose. First, I discuss the nature of constructivist curriculum, contrasting it with traditional approaches based on behaviorist theory. Then I present an example of a problem-solving environment for high school mathematics students. The example illustrates why teachers need help to construct this kind of student-centered curriculum. I provide a scenario of a teacher developing a curriculum using productivity software like TCA, and conclude by discussing some issues I feel will be important in maximizing the effectiveness of the Internet as a medium for the dissemination of innovative curricula for educational reform.
The Problem of Curriculum in Educational Reform
The distribution of curriculum over the Internet and the use of productivity software for searching and adapting posted ideas could benefit any pedagogical approach. However, it is particularly crucial for advancing reform in education.
The barriers to educational reform are legion, as many people since John Dewey have found. Teachers, administrators, parents and students must all be convinced that traditional schooling is not the most effective way to provide an adequate foundation for life in the future. They must be trained in the new sensitivities required. Once everyone agrees and is ready to implement the new approach there is still a problem: what activities and materials should be presented on a day to day basis? This concrete question is the one that Internet sharing can best address. I generalize the term curriculum to cover this question.
Consider curricula for mathematics. Here, the reform approach is to emphasize the qualitative understanding of mathematical ways of thinking, rather than to stress rote memorization of quantitative facts or “number skills.” Behaviorist learning theory supported the view that one method of training could work for all students; reformers face a much more complex challenge. There is a growing consensus among educational theorists that different students in different situations construct their understandings in different ways (Greeno, 1993). This approach is often called constructivism or constructionism (Papert, 1993). It implies that teachers must creatively structure the learning environments of their students to provide opportunities for discovery and must guide the individual learners to reach insights in their own ways.
Behaviorism and constructivism differ primarily in their views of how students build their knowledge. Traditional, rationalist education assumed that there was a logical sequence of facts and standard skills that had to be learned successively. The problem was simply to transfer bits of information to students in a logical order, with little concern for how students acquire knowledge. Early attempts at designing educational software took this approach to its extreme, breaking down curricula into isolated atomic propositions and feeding these predigested facts to the students. This approach to education was suited to the industrial age, in which workers on assembly lines performed well-defined, sequential tasks.
According to constructivism, learners interpret problems in their environments using conceptual frameworks that they developed in the past (Roschelle, 1996). In challenging cases, problems can require changes in the frameworks. Such conceptual change is the essence of learning: one’s understanding evolves in order to comprehend one’s environment. To teach a student a mathematical method or a scientific theory is not to place a set of propositional facts into her mind, but to give her a new tool that she can make her own and use in her own ways in comprehending her world.
Constructivism does not entail the rejection of a curriculum. Rather, it requires a more complex and flexible curriculum. Traditionally, a curriculum consisted of a textual theoretical lesson, a set of drills for students to practice and a test to evaluate if the students could perform the desired behaviors. In contrast, a constructivist curriculum might target certain cognitive skills, provide a setting of resources and activities to serve as a catalyst for the development of these skills and then offer opportunities for students to articulate their evolving understandings (NCTM, 1989). The cognitive skills in math, for example, might include qualitative reasoning about graphs, number lines, algorithms or proofs.
My colleagues on the project and I believe that the movement from viewing a curriculum as fact-centered to viewing it as cognitive-tool-centered is appropriate for the post-modern (post-industrial, post-rationalist, post-behaviorist) period. Cognitive tools include, importantly, alternative knowledge representations (Norman, 1993). As researchers in artificial intelligence, we know that knowledge representations are key to characterizing or modeling cognition. We have also found that professionals working in typical contemporary occupations focus much of their effort on developing and using alternative knowledge representations that are adapted to their tasks (Sumner, 1995). Curricula to prepare people for the next generation of jobs would do well to familiarize students with the creation and use of alternative conceptual representations.
A Diverse Learning Ecology
Teachers need help to create learning environments that stimulate the construction and evolution of understanding through student exploration using multiple conceptual representations. A stimulating learning environment is one with a rich ecology, in which many elements interact in subtle ways. In this section I present an illustration of a rich ecology for learning mathematical thinking that includes: inductive reasoning, recursive computation, spreadsheet representation, graphing, simultaneous equations and programming languages.
 A typical curriculum suggestion that might be
posted on an educational resources listing on the Internet is the problem of regions of a circle: Given n points on the circumference of a circle, what is
the maximum number of regions one can divide the circle into by drawing
straight lines connecting the points? (See figure 1-1.) For instance,
connecting two points divides the circle into two regions; connecting three
points with three lines creates four regions. This is a potentially fascinating
problem because its subtleties can be explored at length using just algebra and
several varieties of clear thinking.
A typical curriculum suggestion that might be
posted on an educational resources listing on the Internet is the problem of regions of a circle: Given n points on the circumference of a circle, what is
the maximum number of regions one can divide the circle into by drawing
straight lines connecting the points? (See figure 1-1.) For instance,
connecting two points divides the circle into two regions; connecting three
points with three lines creates four regions. This is a potentially fascinating
problem because its subtleties can be explored at length using just algebra and
several varieties of clear thinking.
Figure 1-1 goes approximately here
The problem with this curriculum offering as an Internet posting is that it has not been placed in a rich setting. To be useful, a fuller curriculum providing a set of conceptual tools is needed. For instance, a discussion of inductive reasoning brings out some of the character of this particular problem. If one counts the number of regions, R(n), for n = 1 to 6, one obtains the doubling series: 1, 2, 4, 8, 16, 31. Almost! One expects the last of these numbers to be 32, but that last region is nowhere to be found. For larger n, the series diverges completely from the powers of 2. Why? Here, inductive reasoning can come to the rescue of the hasty inductive assumption—if, that is, the problem is accompanied by a discussion of inductive reasoning.
Consider the general case of n points. Assume that the answer is known for n-1 points and think about how many new regions are created by adding the n-th point and connecting it to each of the n-1 old points. There is a definite pattern at work here. It may take a couple days of careful thought to work it out. It would also help if the sigma notation for sums of indexed terms is explained as a representational tool for working on the problem. Perhaps a collaborative group effort will be needed to check each step and avoid mistakes.
At this point, a teacher might introduce the notion of recursion and relate it to induction. If the students can program in Logo or Pascal (programming languages that can represent recursive processes), they could put the general formula into a simple but powerful program that could generate results for hundreds of values of n very quickly without the tedious and error-prone process of counting regions in drawings. It would be nice to formalize the derivation of this result with a deductive proof, if the method of formulating proofs has been explained.
Now that students are confident that they have the correct values for many n, they can enter these values in a spreadsheet to explore them. The first representation they might want to see is a graph of R(n) vs. n. On the spreadsheet they could make a column that displays the difference between each R(n) and its corresponding R(n-1). Copying this column several times, they would find that the fourth column of differences is constant. This result means that R(n) follows a fourth order equation, which can be found by solving simultaneous equations.
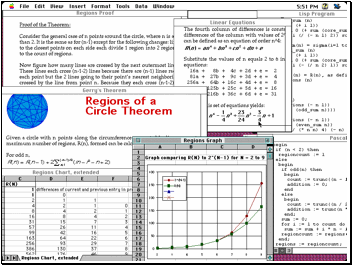
Figure 1-2. A number of multimedia resources related to the “regions of a circle” problem. These include textual documents, drawings, equations, spreadsheets, graphs and computer program source code.
The point of this example is that sharing the isolated statement of the problem is not enough. The rich learning experience involves being introduced to alternative representations of the problem: induction, recursion, spreadsheet differences, graphs, computer languages, simultaneous equations, etc. There is not one correct method for tackling a problem like this; a mathematically literate person needs to be able to view the problem’s many facets through several conceptual frameworks.
A curriculum in the new paradigm typically consists of stimulating problems immersed in environments with richly interacting ecologies, including: cognitive skills, knowledge representations, computational tools, related problems and reference materials. Perhaps a creative teacher with unlimited preparation time could put these materials together. However, the reality is that teachers deserve all the support they can get if they are to prepare and present the complex learning ecologies that constructivist reforms call for. Computer support for curriculum development should make the kinds of resources shown in figure 1-2 readily available.
Figure 1-2 goes approximately here
From Database to Design Environment
Curriculum planning for learning ecologies is not a simple matter of picking consecutive pages out of a standard textbook or of working out a sequential presentation of material that builds up to fixed learning achievements. Rather, it is a matter of design. To support teachers in developing curriculum that achieves this, we must go beyond databases of isolated resources to provide design environments for curriculum development.
It may seem to be an overwhelming task to design an effective learning environment for promoting the development of basic cognitive skills. However, dozens of reform curricula have already been created. The problem now is to disseminate these in ways that allow teachers to adapt them to their local needs and to reuse them as templates for additional new curricula. It is instructive to look at a recent attempt to make this type of curriculum available. The “MathFinder CD-ROM: a collection of resources for mathematics reform” excerpts materials from thirty new math curricula (Kreindler & Zahm, 1992). Like the posting of curriculum ideas at several Internet sites, this is an important early step at electronic dissemination.
Unfortunately, MathFinder has a number of serious limitations due to its CD-ROM (read-only) format. It relies on a fixed database of resources that allows resources to be located but not expanded or revised. Its indexing is relatively simple¾primarily oriented toward illustrating a particular set of math standards¾yet its search mechanism is cumbersome for many teachers. Because its resources are stored in bitmap images, they cannot be adapted in any way by teachers or students. Moreover, MathFinder provides no facility for organizing resources into curricula¾despite the fact that most of the resources it includes are excerpted from carefully constructed curricula. Because it is sold as a read-only commodity, MathFinder does not allow teachers to share their experiences with annotations or to add their own curricular ideas. Thus, of the five issues listed in the Introduction of this study, MathFinder only provides a partial solution to the issues of location and search.
An alternative approach is suggested by our work on domain-oriented design environments (Fischer et al., 1993; Fischer et al., 1998; Repenning & Sumner, 1995; Stahl, McCall, & Peper, 1992; Stahl, 1993). A software design environment provides a flexible workspace for the construction of artifacts, and places useful design tools and materials close at hand. A design environment for curriculum development goes substantially beyond a database of individual resources. Based on this approach, we built a prototype version of a Teacher’s Curriculum Assistant (TCA). TCA includes a catalog of previously designed curricula that can be reused and modified. It has a gallery of educational resources that can be inserted into partial curriculum designs. There is a workspace, into which curricula from the catalog can be loaded and resources from the gallery inserted. It is also possible for a teacher to specify criteria for the desired curriculum. Specifications are used for searching the case-base of curricula, adapting the resources and critiquing new designs.
TCA allows teachers to download curricular resources from the Internet and to create coherent classroom activities tailored to local circumstances. In particular, TCA addresses the set of five issues identified in the Introduction:
1. TCA is built on a database of information about educational resources posted to the Internet, so it provides a mechanism for teachers to locate sources of curriculum ideas at scattered Internet sites.
2. The TCA database indexes each resource in a uniform way, allowing teachers to search for all items meeting desired conditions.
3. TCA includes tools to help teachers adapt items they find to the needs of their classroom.
4. TCA provides a design workspace for organizing retrieved ideas into lesson plans that build toward long-term goals.
5. TCA lets teachers conveniently share their experiences back through the Internet.
The TCA Prototype
Based on preliminary study of these issues, a TCA prototype has been developed. Six interface screens have been designed for teacher support: Profiler, Explorer, Versions, Editor, Planner, and Networker.
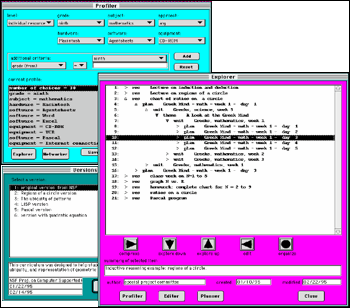
Figure 1-3. The teacher-client software interface for locating, searching and selecting resources and curricula: the Profiler, Explorer and Versions.
The Profiler, Explorer and Versions interfaces work together for information retrieval (figure 1-3). The Profiler helps teachers define classroom profiles and locates curricula and resources that match the profile. The Explorer displays these items and allows the teacher to search through them to find related items. Versions then helps the teacher select from alternative versions that have been adapted by other teachers. Through these interfaces, teachers can locate the available materials that most closely match their personal needs; this makes it easier to tailor the materials to individual requirements.
Figure 1-3 goes approximately here
The Planner, Editor and Networker help the teacher to prepare resources and curricula, and to share the results of classroom use (figure 1-4). The Planner is a design environment for reusing and reorganizing lesson plans. The Editor allows the teacher to modify and adapt resources. This is a primary means of personalizing a curriculum to individual classroom circumstances. Finally, the Networker supports interactions with the Internet, providing a two-way medium of communication with a global community of teachers. Using the Networker, a teacher can share personalized versions of standard curricula with other teachers who might have similar needs.
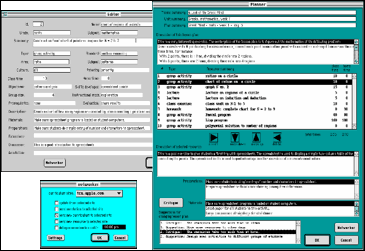
Figure 1-4. The teacher-client interface for adapting, organizing and sharing resources and curricula: the Planner, Editor and Networker.
Figure 1-4 goes approximately here
To illustrate how TCA works, each of the five issues will be discussed in the following sections. These sections present a scenario of a teacher using TCA to locate resources, search through them, adapt selected resources, organize them into a curriculum and share the results with other teachers.
Scenario Step 1: Locating Curriculum
Imagine a high school mathematics teacher using TCA. In the coming year she has to introduce some geometric concepts like Pythagoras’ Theorem and deductive proofs. More generally, she might want to discuss the ubiquity of patterns and ways to represent them mathematically. TCA lets her browse for semester themes and their constituent weekly units and lesson plans related to these topics.
TCA distinguishes four levels of curricula available on the Internet:
Š A theme is a major curriculum, possibly covering a semester or a year of school and optionally integrating several subjects. A theme consists of multiple teaching units.
Š A weekly unit is part of a theme, typically one week of lessons for a single subject. A unit is described by its constituent daily lesson plans.
Š A plan is one day’s lesson for a class. A lesson plan might include a number of resources, such as a lecture, a reading, an exercise or project, and perhaps a quiz and a homework assignment.
Š A resource is an element of a lesson plan. It might be a text, available as a word processing document. It could also be a video clip, a spreadsheet worksheet, a graphic design or a software simulation. Resources are the smallest units of curricula indexed by TCA.
TCA lets the teacher locate relevant curricula by analyzing information stored on her computer about items available on the Internet. Along with the TCA software on her computer there is a case-base of summaries (indexes) of curricula and resources that can be downloaded. These summary records reference curricula and resources that have been posted to Internet nodes around the world. In addition to containing the Internet address information needed for downloading an item, a record contains a description of the item, so that the teacher can decide whether or not it is of interest.
After a set of interesting items has been selected based on the information in the case-base, TCA downloads the items to the teacher’s computer. This happens without her having to know where they were located or how to download them. The items are then available for modification, printing or distribution to her students. If Internet traffic is slow, she may opt to download batches of curriculum and resources overnight and then work with them the next day.[1]
Scenario Step 2: Searching for Resources
TCA provides a combination of query and browsing mechanisms to help a teacher select curricula of interest and to find resources that go with it. She can start in the Profiler (Figure 3) by specifying that she wants a curriculum for ninth grade mathematics. Then she can browse through a list of themes in the Explorer that meet the specification. If the list is too long, she can narrow down her search criteria.
The theme named “A Look at the Greek Mind” is summarized as: “This is an integrated curriculum that explores myth, patterns and abstract reasoning.” It emphasizes patterns and is likely to include Pythagoras’ theorem. The teacher can click on this theme in the list. Her computer now displays summaries of the units that make up the curriculum for that theme. This list shows three weekly units. Select week 1, described as “Abstract thinking: number theory and deductive reasoning.”
She now sees summaries of that week’s five daily lesson plans. She looks at the geometry example for day 3, “Inductive reasoning example: regions of a circle.” She select that one and the screen changes to show the lesson plan in the Planner (Figure 4). It lists all the resources suggested for that period: two lecture topics, a class exercise, several alternative activities for small groups and a homework assignment.
The screenshot of Explorer illustrates how a teacher can browse from a given resource, like “chart of regions on a circle” up to all the lesson plans, units and themes that include that resource and then back down to all the associated units, plans and resources. This is one way to locate related resources within curricular contexts. The teacher can also turn to the Versions component to find variations on a particular resource and comments about the resource and its different versions by teachers who have used it.
Notice resource #2 in the Planner, where students create a spreadsheet chart: “Group activity: Chart of ratios on a circle.” When the teacher selects it with the mouse, the Editor shows the detail for that resource, including its index values.
The description contained in the case-base for each posted resource is organized as a set of 24 indexes and annotations, such as: recommended grade level, content area, pedagogical goal, instructional mode, prerequisites, materials used, required time and the like. Note that total class time and homework time are computed and teacher preparations for the resources are listed below the workspace.
The TCA Profiler allows a teacher to specify her curricular needs using combinations of these indexes. Resources are also cross referenced so that she can retrieve many different resources that are related to a given one. Thus, once she has found the “problem of regions of a circle”, she can easily locate discussions of inductive reasoning, formal proofs, recursion, simultaneous equations, sample programs in Logo or Pascal, spreadsheet templates for analyzing successive differences and graphing tools. She can also find week-long units that build on geometric problems like this one, with variations for students with different backgrounds, learning styles or interests. TCA allows her to search both top-down from themes to resources and bottom-up from resources to curricula.
Scenario Step 3: Adapting to Local Needs
Adaptation tools are available in TCA for resources that have been downloaded from the Internet. The Planner component provides a design workspace for assembling a custom lesson plan and the Editor helps a teacher to adapt individual resources to her local needs. The TCA system can often make automated suggestions for adapting a resource to the specification given in the search process. For instance, if she retrieves a resource that was targeted for 11th grade when she is looking for 10th grade material, then TCA might suggest allowing her students more time to do the tasks or might provide more supporting and explanatory materials for them. In general, she will need to make the adaptations; even where the software comes up with suggestions, she must use her judgment to make the final decision.
While TCA can automate some adaptation, most tailoring of curricula requires hands-on control by an experienced teacher. Sometimes TCA can support her efforts by displaying useful information. For instance, if she is adapting resources organized by national standards to local standards she might like her computer to display both sets of standards and to associate each local standard with corresponding national standards. In other situations, perhaps involving students whose first language is not English, TCA might link a resource requiring a high level of language understanding to a supplementary visual presentation.
The adaptation process relies on alternative versions of individual resources being posted. The TCA VERSIONS component helps a teacher adjust to different student groups, teaching methods and time constraints by retrieving alternative versions of resources that provide different motivations, use different formats or go into more depth. She can substitute these alternative resources into lesson plans; they can then be modified with multimedia editing software from within TCA.
Included in the Editor is a reduced image of the spreadsheet itself. If a teacher click on this image, TCA brings up the commercial software application in which the document was produced. So she can now edit and modify the copy of this document which appears on her screen. She need not leave TCA to do this. Then she can print out her revised version for her students or distribute it directly to their computers. In this way, she can use her own ideas or those of her students to modify and enhance curricular units found on the Internet.
Just as it is important for teachers to adapt curricula to their needs, it is desirable to have resources that students can tailor. Current software technology makes this possible, as illustrated by a number of simulations in the Agentsheets Exploratorium (Ambach, Perrone, & Reppening, 1995; Stahl, Sumner, & Repenning, 1995).
Scenario Step 4: Organizing Resources into Lesson Plans
The lesson plan is a popular representation for a curriculum. It provides teachers a system for organizing classroom activities. TCA uses the lesson plan metaphor as the basis for its design workspace. A teacher can start her planning by looking at downloaded lesson plans and then modifying them to meet her local needs.
The TCA Planner workspace for designing lesson plans was shown in Figure 4. In addition to summaries of each resource, the workspace lists the time required by each resource, both in class and at home. These times are totaled at the bottom of the list of resources in the Planner. This provides an indication of whether there is too much or too little instructional material to fill the period. The teacher can then decide to add or eliminate resources or adjust their time allowances. The total homework time can be compared to local requirements concerning homework amounts.
TCA incorporates computational critics (Fischer et al., 1993; Fischer et al., 1998). Critics are software rules that monitor the curriculum being constructed and verify that specified conditions are maintained. For instance, critics might automatically alert the teacher if the time required for a one-day curriculum exceeds or falls short of the time available.
Scenario Step 5: Sharing New Experiences
Once a teacher has developed curricula and used them successfully in the classroom, she may want to share her creations with other teachers. This way, the pool of ideas on the Internet will grow and mature. TCA has facilities for her to annotate individual resources and curricular units at all levels with descriptions of how they worked in her classroom. This is part of the indexing of the resource or unit.
Assume that a teacher downloaded and used the “regions of a circle” resource and modified it based on her classroom experience. Now she wants to upload her version back to the Internet. The TCA Networker component automates that process, posting the new resource to an available server and adding the indexes for it to the server used for distributing new indexes. Because the indexing of her revision would be similar to that of the original version of the resource, other teachers looking at the “regions of a circle” resource would also find her version with her comments. In this way, the Internet pool of resources serves as a medium of communication among teachers about the specific resources. It is in such ways that I hope the use of the Internet for curriculum development will go far beyond today’s first steps.
What I Have Learned
I conceptualize the understanding I have reached through my work on TCA in five principles:
1. Most resources should be located at distributed sites across the Internet, but carefully structured summaries (indexes) of them should be maintained on teachers’ local computers or in centralized catalogs.
2. The search process should be supported through a combination of query and browsing tools that help teachers explore what is available.
3. Adaptation of tools and resources to teachers and students is critical for developing and benefiting from constructivist curriculum.
4. Resources must be organized into carefully designed curriculum units to provide effective learning environments.
5. The Internet should become a medium for sharing curriculum ideas, not just accessing them.
A system to assist teachers in developing curricula for educational reform has been designed and prototyped. All aspects of the system must now be refined by working further with classroom teachers and curriculum developers. While the approach of TCA appeals to teachers who have participated in its design, its implementation must still be tuned to the realities of the classroom.
The distribution of resources and indexes prototyped in TCA has attractive advantages. Because the actual multimedia resources (text, pictures, video clips, spreadsheet templates, HyperCard stacks, software applications) are distributed across the Internet, there is no limit to the quantity or size of these resources and no need for teachers to have large computers. Resources can be posted on network servers maintained by school districts, regional educational organizations, textbook manufacturers and other agencies. Then the originating agency can maintain and revise the resources as necessary.
However, the approach advocated here faces a major institutional challenge: the standardization of resource indexing. The difficulty with this approach is the need to index every resource and to distribute these indexes to every computer that runs TCA. This involves (a) implementing a distribution and updating system for the case-base index records and (b) establishing the TCA indexing scheme as a standard.
The distribution and updating of indexes can be handled by tools within TCA and support software for major curriculum contributors. However, the standardization requires coordination among interested parties. Before any teachers can use TCA there must be useful indexed resources available on the network, with comprehensive suggested lesson plans. It is necessary to establish cooperation among federally-funded curriculum development efforts, textbook publishers, software publishers and school districts. If successful, this will establish a critical mass of curriculum on the Internet accessible by TCA. Then the Internet can begin to be an effective medium for the global sharing of locally adaptable curriculum.