To understand the data in this workshop, it is necessary to have personal experience with dynamic geometry. Take a few minutes now at a computer to try GeoGebra. If you can do this collaboratively, discussing each step with a friend, that would be ideal.
1. First, watch a two-minute video on constructing an equilateral triangle in GeoGebra, such as the one at www.youtube.com/watch?v=ORIaWNQSM_E.
2. Then download GeoGebra from www.GeoGebra.org and open it up.
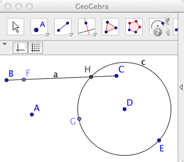
3. Try the basic geometry tools. Construct a point with the point tool. Use the move tool to drag it around. Construct a line segment with the segment tool and drag it. Construct a circle with the circle tool. Construct a new point on your line segment and one on your circle; drag these points. What happens? Move your line to cross your circle and construct a new point where they intersect (see point H in Figure 1). Can you move your new point directly or indirectly?

Figure 1. Free, partially constrained and completely dependent points.
4. Try to construct an equilateral triangle yourself. Use the “File” | “New” menu item to clear the work area. Start with a base side AB. Then draw circles of radius AB centered on endpoints A and B, respectively. Construct point C at an intersection of these circles. Use the polygon tool to construct triangle ABC. Drag the vertices—this is the “drag test.” Do you see why the triangle remains equilateral dynamically? The position of point C is dependent upon the circles, which are dependent upon the segment AB.
5. Now, download the file inscribe.ggb from www.GerryStahl.net/vmt/inscribe.ggb or from www.geogebratube.org/material/show/id/43056. Follow the directions (as in Figure 2.) Drag points A and D to explore the figure and discover its built in dependencies. How would you describe the geometry of this figure?
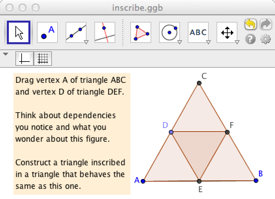
Figure 2. The inscribed triangles challenge problem.
6. The challenge is to create a figure like this. Your version should behave dynamically the same as the given figure. Use the drag test to see if it does. This is a challenging problem. Do not worry if you cannot do it now. You will see in the workshop how a virtual math team figured it out.
Hint: You already know how to create the outer triangle, ABC. Start with that. Construct a point on one side of the outer triangle. This will be one vertex of the inner triangle. Can you use the same method to create the inner triangle? Try it. Does it satisfy the required dependencies?